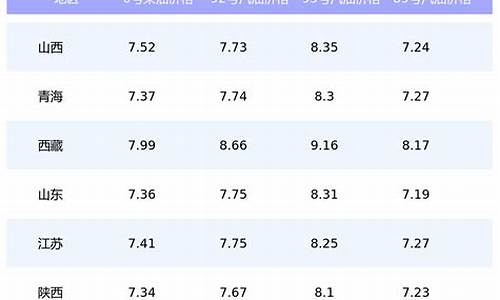
油价调价规则_油价调整的算法是什么意思

1.汽车油耗一百公里8.5升 油价是7.1怎么算

2.石油市场价格抓取算法

郎咸平又在造谣行骗、蛊惑人心、吸引眼球。为的是推销烂书《我们的生活为什么这么无奈》

郎咸平说：我们的油价就是全世界最贵的。他又在造谣了。

美国报纸说中国油价低：“一加仑汽油在北京只卖2.6美元，还不到美国的一半。”又说，“中国现在是世界上油价最低的国家之一，只相当于美国的61%，日本的41%、英国的28%……”

质问郎咸平：一贯对美国膜顶礼拜的郎咸平为什么现在不提美国说法呢？

所谓中国油价世界最贵的算法是：油价6.3元、高速公路过路费8.33元、养路费1.08元。

质问1.：郎咸平你明明知道高速公路和养路费没有到是中石油、中石化口袋，你为什么闭着眼说瞎话？

郎咸平说国际油价跌的时候你（中石油、中石化）不跌，国际油价涨的时候你却使劲涨？

质问2：国际油价，每时不同样。你是真傻？还是傻？你是不是要给每个加油站配一个油价翻牌工？你真的不知道国内成品油“22+4%”的调价条件？还是明知故问？

老百姓希望油价越低越好。你迎合这一心理，睁着眼睛说瞎话。还总是：总是说：在《我们的生活为什么这么无奈》中给出了明确答案。好像自己是先知先觉。明眼人一看便知他为了卖你的烂书，真是不择手段、不要×脸。什么教授、博士。 简直就是狗屎！！

狗屎！狗屎！狗屎！狗屎！狗屎！狗屎！狗屎！狗屎！狗屎！

臭不可闻！臭不可闻！臭不可闻！臭不可闻！臭不可闻！

汽车油耗一百公里8.5升 油价是7.1怎么算

队列是一种先进先出的数据结构，由于这一规则的限制，使得队列有区别于栈等别的数据结构。

作为一种常用的数据结构，同栈一样，是有着丰富的现实背景的。以下是几个典型的例子。

[例5-2] 一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(设出发时油箱是空的).给定两个城市之间的距离D1,汽车油箱的容量C(以升为单位),每升汽油能行驶的距离D2,出发点每升汽油价格P和沿途油站数N(N可以为零),油站i离出发点的距离Di,每升汽油价格Pi(i=1,2,……N).

计算结果四舍五入至小数点后两位.

如果无法到达目的地,则输出"No Solution".

样例:

INPUT

D1=275.6 C=11.9 D2=27.4 P=2.8 N=2

油站号I

离出发点的距离Di

每升汽油价格Pi

1

102.0

2.9

2

220.0

2.2

OUTPUT

26.95(该数据表示最小费用)

[问题分析]

看到这道题,许多人都马上判断出穷举是不可行的,因为数据都是以实数的形式给出的.但是,不用穷举,有什么方法是更好的呢 递推是另一条常见的思路,但是具体方法不甚明朗.

既然没有现成的思路可循,那么先分析一下问题不失为一个好办法.由于汽车是由始向终单向开的,我们最大的麻烦就是无法预知汽车以后对汽油的需求及油价变动;换句话说,前面所买的多余的油只有开到后面才会被发觉.

提出问题是解决的开始.为了着手解决遇到的困难,取得最优方案,那就必须做到两点,即只为用过的汽油付钱;并且只买最便宜的油.如果在以后的行程中发现先前的某些油是不必要的,或是买贵了,我们就会说:"还不如当初不买."由这一个想法,我们可以得到某种启示:设我们在每个站都买了足够多的油,然后在行程中逐步发现哪些油是不必要的,以此修改我们先前的购买,节省资金;进一步说,如果把在各个站加上的油标记为不同的类别,我们只要在用时用那些最便宜的油并为它们付钱,其余的油要么是太贵,要么是多余的,在最终的中会被排除.要注意的是,这里的便宜是对于某一段路程而言的,而不是全程.

[算法设计]由此,我们得到如下算法:从起点起(包括起点),每到一个站都把油箱加满(终点除外);每经过两站之间的距离,都按照从便宜到贵的顺序使用油箱中的油,并计算花费,因为这是在最优方案下不得不用的油;如果当前站的油价低于油箱中仍保存的油价,则说明以前的购买是不够明智的,其效果一定不如购买当前加油站的油,所以,明智的选择是用本站的油代替以前购买的高价油,留待以后使用,由于我们不是真的开车,也没有为备用的油付过钱,因而这样的反悔是可行的;当我们开到终点时,意味着路上的费用已经得到,此时剩余的油就没有用了,可以忽略.

数据结构用一个队列:存放由便宜到贵的各种油,一个头指针指向当前应当使用的油(最便宜的油),尾指针指向当前可能被替换的油(最贵的油).在一路用一路补充的过程中同步修改数据,求得最优方案.

注意:每到一站都要将油加满,以确保在有解的情况下能走完全程.并设出发前油箱里装满了比出发点贵的油,将出发点也看成一站,则程序循环执行换油,用油的操作,直到到达终点站为止.

本题的一个难点在于认识到油箱中油的可更换性,在这里,突破现实生活中的思维模式显得十分重要.

[程序清单]

program ex5_2(input,output);

const max=1000;

type recordtype=record price,content:real end;

var i,j,n,point,tail:longint;

content,change,distance2,money,use:real;

price,distance,consume:array[0..max] of real;

oil:array [0..max] of recordtype;

begin

write('Input DI,C,D2,P:'); readln(distance[0],content,distance2,price[0]);

write('Input N:'); readln(n); distance[n+1]:=distance[0];

for i:=1 to n do

begin

write('Input D[',i,'],','P[',i,']:');

readln(distance[i],price[i])

end;

distance[0]:=0;

for i:=n downto 0 do consume[i]:=(distance[i+1]-distance[i])/distance2;

for i:=0 to n do

if consume[i]>content then

begin writeln('No Solution'); halt end;

money:=0; tail:=1; change:=0;

oil[tail].price:=price[0]*2; oil[tail].content:=content;

for i:=0 to n do

begin

point:=tail;

while (point>=1) and (oil[point].price>=price[i]) do

begin

change:=change+oil[point].content;

point:=point-1

end;

tail:=point+1;

oil[tail].price:=price[i];

oil[tail].content:=change;

use:=consume[i]; point:=1;

while (use>1e-6) and (point=oil[point].content

then begin use:=use-oil[point].content;

money:=money+oil[point].content*oil[point].price;

point:=point+1 end

else begin oil[point].content:=oil[point].content-use;

money:=money+use*oil[point].price;

use:=0 end;

for j:=point to tail do oil[j-point+1]:=oil[j];

tail:=tail-point+1;

change:=consume[i]

end;

writeln(money:0:2)

end.

[例5-3] 分油问题:设有大小不等的3个无刻度的油桶,分别能够存满,X,Y,Z公升油(例如X=80,Y=50,Z=30).初始时,第一个油桶盛满油,第二,三个油桶为空.编程寻找一种最少步骤的分油方式,在某一个油桶上分出targ升油(例如targ=40).若找到解,则将分油方法打印出来;否则打印信息"UNABLE"等字样,表示问题无解.

[问题分析] 这是一个利用队列方法解决分油问题的程序.分油过程中,由于油桶上没有刻度,只能将油桶倒满或者倒空.三个油桶盛满油的总量始终等于开始时的第一个油桶盛满的油量.

[算法设计] 分油程序的算法主要是,每次判断当前油桶是不是可以倒出油,以及其他某个油桶是不是可以倒进油.如果满足以上条件,那么当前油桶的油或全部倒出,或将另一油桶倒满,针对两种不同的情况作不同的处理.

程序中使用一个队列Q,记录每次分油时各个油桶的盛油量和倾倒轨迹有关信息,队列中只记录互不相同的盛油状态(各个油桶的盛油量),如果程序列举出倒油过程的所有不同的盛油状态,经考察全部状态后,未能分出TARG升油的情况,就确定这个倒油问题无解.队列Q通过指针front和rear实现倒油过程的控制.

[程序清单]

program ex5_3(input,output);

const maxn=5000;

type stationtype=array[1..3] of integer;

elementtype=record

station:stationtype;

out,into:1..3;

father:integer

end;

queuetype=array [1..maxn] of elementtype;

var current,born:elementtype;

q:queuetype;

full,w,w1:stationtype;

i,j,k,remain,targ,front,rear:integer;

found:boolean;

procedure addQ(var Q:queuetype;var rear:integer; n:integer; x:elementtype);

begin

if rear=n

then begin writeln('Queue full!'); halt end

else begin rear:=rear+1; Q[rear]:=x end

end;

procedure deleteQ(var Q:queuetype;var front:integer;rear,n:integer;var x:elementtype);

begin

if front=rear

then begin writeln('Queue empty!'); halt end

else begin front:=front+1; x:=Q[front] end

end;

function dup(w:stationtype;rear:integer):boolean;

var i:integer;

begin

i:=1;

while (i<=rear) and ((w[1]q[i].station[1]) or

(w[2]q[i].station[2]) or (w[3]q[i].station[3])) do i:=i+1;

if i0 then

begin

print(q[k].father);

if k>1 then write(q[k].out, ' TO ',q[k].into,' ')

else write(' ':8);

for i:=1 to 3 do write(q[k].station[i]:5);

writeln

end

end;

begin {Main program}

writeln('1: ','2: ','3: ','targ');

readln(full[1],full[2],full[3],targ);

found:=false;

front:=0; rear:=1;

q[1].station[1]:=full[1];

q[1].station[2]:=0;

q[1].station[3]:=0;

q[1].father:=0;

while (front begin

deleteQ(q,front,rear,maxn,current);

w:=current.station;

for i:=1 to 3 do

for j:=1 to 3 do

if (ij) and (w[i]>0) and (w[j]remain

then begin w1[j]:=full[j]; w1[i]:=w[i]-remain end

else begin w1[i]:=0; w1[j]:=w[j]+w[i] end;

if not(dup(w1,rear)) then

begin

born.station:=w1;

born.out:=i;

born.into:=j;

born.father:=front;

addQ(q,rear,maxn,born);

for k:=1 to 3 do

if w1[k]=targ then found:=true

end

end

end;

if not(found)

then writeln('Unable!')

else print(rear)

end.

石油市场价格抓取算法

油耗的计算为：油耗x油价/100公里。百公里8.5升，按照7块钱一升来算，那么大概需要?60，也就是说每公里六毛钱左右。

设油箱红灯亮了去加油，加的是92号汽油，单价是6.2元/L，加满后总共用了300块（这里不讲你油箱多少L）。然后你归零公里数，从0公里开始算，等到下次红灯再亮时去加油。此时车子显示你一共跑了 480公里，加了290元，那么我们就得到数据290元跑了480公里。

百公里油耗，就是290元/480公里=0.6 0.6*100=60 60/6.2（油的单价）=9.67L 。

每公里就是290元/480公里=0.6。

每个人的车型不同，性能不同，油耗自然就会不一样，但是算法都是一样的，只要记住初始里程数和结束里程数，就能够算出自己车辆的油耗，但是往往这个实际油耗会比官方给出的油耗要高出一部分。

因为官方给出的数据都是理想状态的，比如一个驾驶员按照一定速度行驶一百公里的油耗，由于多数车辆在90公里/小时接近经济车速，所以大多数官方给出的油耗都是90公里/小时的百公里油耗，这完全就是理想状态。

百度百科-油耗

由于网站上的石油市场价格历史数据的时间粒度从年一直精确到日，所有的下载靠人工完成是很困难的，而且由于下载到本地之后的表格字段并不规范，所以必须要根据数据库字段的要求对字符串和Excel表格操作，使之规范化后再入库。其难点在于实现石油市场价格的自动抓取完成对数据源的自动下载，数据源的自动更新，与管理平台的无缝链接，以及ActiveX 插件的制作。

5.3.1.1 数据源的自动下载

石油市场价格数据有3个数据源，包括美国能源部能源信息署（EIA）、《华尔街日报》（WJS）和中石油（CNPC）的数据。这些数据源皆为互联网上的。针对3个不同的数据源的特点，用远程自动下载及规范化，以及基于正则表达式的网页数据自动抓取两种不同的技术完成。

（1）远程自动下载及规范化

对于美国能源部网站的油价历史数据，通过设计自动下载引擎，完成对其历史油价数据的自动远程下载，按照指定路径保存到本地，并将每次下载的结果保存到数据库下载日志表；将下载下来的数据进行清洗、转换并上载到中心数据库。

（2）基于正则表达式的网页数据自动抓取技术

由于大部分网页数据并没有提供下载的通道，而且油价数据同股价数据一样更新频率很高。因此需要对网站上的数据进行基于正则表达式网页数据自动抓取。华尔街油价数据、美国能源部上的油价、中石油网页上的油价数据，均需要通过正则表达式的网页自动抓取功能来实现。

网页抓取需要解决的问题：

1）得到需要抓取的网页的地址列表（URL）;

2）根据网页的地址去请求，得到网页的内容；

3）分析网页（HTM L）的结构，并提取出需要的内容，即使用网页结构化信息抽取技术或元数据集技术。可以使用基于字符串查找定位和基于DOM（Document Object Model）结构的分析；数据抓取结构体系，如图5.27所示。

图5.27 B/S网页抓取结构体系

正则表达式的网页数据自动抓取技术涉及网页源码数据的本地化操作，装载源码数据控件的选择，相关信息源码的抓取，源代码的去行操作，数据中含有超链接和字体变换的HTML标签元素的去除，应用零款断言和截取子字符串等字符串函数的方法来抓取数据以及数据入库这些操作（图5.28）。

图5.28 基于正则表达式的网页信息抓取过程

5.3.1.2 数据源的自动更新

当完成对历史数据的初始化之后，需要设计监控引擎，监控网站数据源的更新情况，以决策是否执行增量下载任务。其监控引擎用实时监控技术以及周期性检测技术。当执行增量下载任务之后，需要对下载数据的有效性和完整性进行检查，指定的数据源要定格式、定期进行更新。数据源的自动更新，主要依据站点在对数据更新之后系统能及时发现并自动快速地获取更新。从站点上获取更新的手段，涉及数据更新后的更新超链接、按钮变化后的触发网址的变动，分析网址来获得更新等，如：《华尔街日报》的期货油价就是按照将日期写进网址来制作更新的；若是周末或是节日期间网址同样存在只是网页上无相关内容，于是便要考虑此次更新获得的数据是否有效和存在；另外在处理如AJAX 等网址不变的网络站点或者站点的更新不能从网址上得到解释时，使用针对网页的高级字符串操作来获取更新，前述的正则表达式便是最有效的方法之一。

5.3.1.3 与管理平台的无缝链接

管理平台的功能是要使下载、更新的多个任务按照程式的设计，分配到计算机的几个线程中，通过对线程的调度，达到自动下载和更新的有效管理。为此需要设计审核功能、日志功能、重试次数的阈值，以及开启多个Excel进程的功能。通过审核功能，可以查明自动下载过程中的异常，便于进行人工干预；通过日志功能，可以帮助我们依据日志对任务执行中的错误进行追踪和对出错原因进行判断；通过设置重试次数阈值，可以实现任务执行失败后重试；通过开启多个Excel进程的功能，可以实现EIA的Excel数据自动读取和转换。

5.3.1.4 预测程序ActiveX插件的制作

由于油价预测程序是基于C/S架构开发，要将程序发布到B/S架构必须使用插件技术从服务器端向客户端安装预测程序的核心部件，以达到对油价模型更新而不用再单独编写程序的目的，这样就保证了程序的完整性和解决方案之间的良好衔接。

创建ActiveX插件的过程，必须让系统提供一个接口使得插件能够完整地从后台链接到前台。因为工程无法生成tlb文件，没有tlb文件也就意味着注册失败，以及dll文件或ActiveX 控件在客户端无法使用。创建的类就是通过代码的方式将dll文件在客户端注册，生成tlb文件，使得.exe程序能够在B/S体系下进行操作。